秦九韶方法
编辑:Simone
2025-03-20 06:07:20
599 阅读
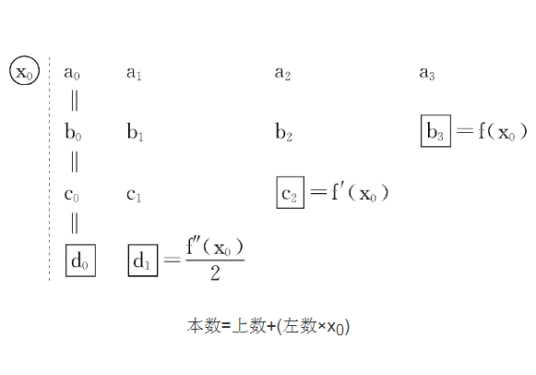
秦九韶方法(Qin Jiushao method)是求实系数多项式实根近似值的一种方法。例如,设实系数多项式f(x)在[3,4]内有一实根α,令x=3+y,即y=x-3,再令f1(y)=f(3+y),则f1(y)在[0,1]内有一个相应的实根,把[0,1]分为十个小的区间[0,0.1],[0.1,0.2],…,[0.9,1],看f1(y)的相应实根在哪个区间内,比如在[0.7,0.8]内,令y=0.7+z,z=y-0.7,设f2(z)=f1(0.7+z),则f2(z)在[0,0.1]内必有相应的一个实根,同样,把[0,0.1]分成十个小区间[0,0.01],[0.01,0.02],…,[0.09,0.1],看f2(z)的相应实根在哪个区间内,比如在[0.04,0.05]内,于是α∈[3.74,3.75],则3.74与3.75就是f(x)的实根α精确到0.01的近似值,前者是不足近似值,后者是过剩近似值,如此下去,可达到所需要的精确度。这个方法是秦九韶于1247年在他所著《数书九章》一书中给出的,有不少书称为霍纳-鲁菲尼方法,实际上鲁菲尼(P.Ruffini)在1804年,霍纳(W.G.Horner)在1819年才分别提出这一方法 。
想要了解更多“秦九韶方法”的信息,请点击:秦九韶方法百科
版权声明:本站【百问十九】文章素材来源于网络或者用户投稿,未经许可不得用于商用,如转载保留本文链接:https://www.baiwen19.com/answer/200681.html



